Несколько простых функций: оценка площади треугольника
Мы также можем оценить площадь треугольника. Здесь Вам пригодится формула Герона:
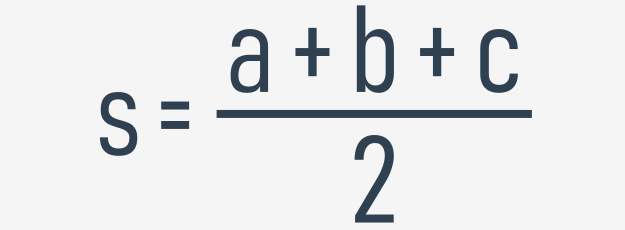
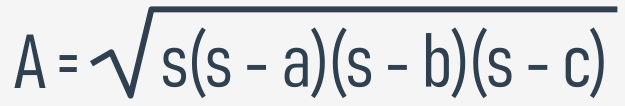
Мы собираемся использовать оператор возведения в степень, чтобы найти квадратный корень - это может показаться странным, но оно работает:
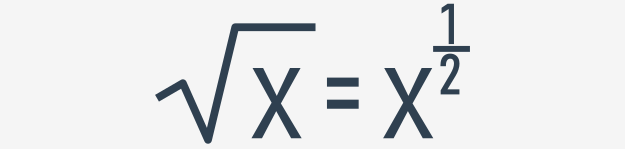
Вот конечный код:
def is_a_triangle(a, b, c):
return a + b > c and b + c > a and c + a > b
def heron(a, b, c):
p = (a + b + c) / 2
return (p * (p - a) * (p - b) * (p - c)) ** 0.5
def area_of_triangle(a, b, c):
if not is_a_triangle(a, b, c):
return None
return heron(a, b, c)
print(area_of_triangle(1., 1., 2. ** .5))
Пробуем это с прямоугольным треугольником как половиной квадрата с одной стороной, равной 1. Это означает, что его площадь должна быть равна 0,5.
Это странно - код дает следующий вывод:
0.49999999999999983
output
Это очень близко к 0,5, но это не совсем 0,5. Что это значит? Это ошибка?
Нет, это не так. Это особенности вычислений с плавающей запятой. Мы скоро расскажем об этом подробнее.
Code
def is_a_triangle(a, b, c):return a + b > c and b + c > a and c + a > b
a = float(input('Enter the first side\'s length: '))
b = float(input('Enter the second side\'s length: '))
c = float(input('Enter the third side\'s length: '))
if is_a_triangle(a, b, c):
print('Yes, it can be a triangle.')
else:
print('No, it can\'t be a triangle.')
{{ dockerServerErrorMsg }}
×
{{ errorMsg }}
×
{{ successMsg }}
×